Parity #

Previously we mentioned that we can describe states of a Rubik’s Cube using elements of symmetric groups, or permutations. In general, permutations are key to group theory; there’s a theorem called Cayley’s Theorem that states that any group is the same as a subgroup of $S_n$, where $n$ is the number of elements in the group. While we aren’t covering Cayley’s Theorem, notice that if any group can be expressed using permutations, in a sense, understanding permutations perfectly is akin to understanding group theory. Parity, the concept we are going to cover today will help us understand permutations deeper.

Tranpositions #

A transposition is a 2-cycle. In other words, a single swapping of elements. For instance, in $S_4$, $(1 \ 2)$, or swapping the first and second elements, is a valid transposition.

Transpositions are important because every permutation can be broken down into a product of transpositions, and the parity of the number of transpositions in a permutation is always preserved. We will briefly show how a permutation can be written as a product of transpositions. Recall every permutation can be written as a product of disjoint cycles. Then given a cycle $(a_1 \ a_2 … \ a_m),$ we can write this in the following equivalent way: $$(a_1 \ a_2 … \ a_m) = (a_1 \ a_m)(a_1 \ a_{m-1})…(a_1 \ a_3) (a_1 \ a_2).$$ Try tracking an arbitrary element $a_i$. In the cycle given on the left, $a_i$ goes directly to $a_{i+1}$. In the cycle on the right, the first time $a_i$ appears is the $(a_1 \ a_i)$ term. So $a_i$ is moved to the $a_1$ position. Then, the next term is $(a_1 \ a_{i+1}),$ meaning it is then moved to the $a_{i+1}$ position, as desired. We can do this argument for any $a_i$ (a special case should be noted for $a_1$ and $a_m.$

Note that this representation is not unique. For instance, in $S_3$ we can write the element $(1 \ 2 \ 3) = (1 \ 3)(1 \ 2) = (1 \ 2)(2 \ 3).$ In fact, we can extend this infinitely by adding additional terms in pairs, as adding $(1 \ 2) (1 \ 2)$ does nothing to the permutation while extending the length of our representation.

Sign is Preserved #

We just said the length of a sequence can vary when written as a product of transpositions. However, the sign of a permutation, or the evenness or oddness of this length, is always preserved. We will not prove this here, but Wikipedia has a variety of proofs which may interest you.

More concretely, any permutation $\sigma$ can be written as a product of transpositions. Suppose that we have one such representation which consists of $n$ transpositions. Then $\epsilon(\sigma) = 1$ if $n$ is even and $\epsilon(\sigma) = -1$ if $n$ is odd. We also say $\sigma$ has even parity if $n$ is even and odd parity if $n$ is odd.

Example #

Consider the permutation $\sigma = (1\ 3\ 4\ 2)$. There are multiple ways we can express this permutations using transpositions.

1. $(1\ 2)(1\ 4)(1\ 3)$

2. $(3\ 4)(2\ 4)(1\ 2)$

3. $(1\ 2)(2\ 4)(1\ 4)(2\ 3)(1\ 2)$

4. $\dots$

Notice that all of these decompositions are odd-length, so $\epsilon(\sigma) = -1$.

Rubik’s Cube and Parity #

Let’s consider the D face of the Rubik’s Cube.

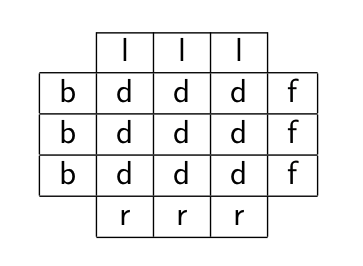
After applying the move D, this is what we get.

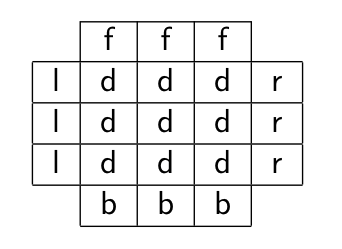
In other words, we can write the D move using the permutation D = (dlf dfr drb dbl)(df dr db dl). The parity of this permutation is 1, in other words we can write D as an even number of transpositions (Try and verify this!).

In fact, all single Rubik’s Cube moves have even parity. Now, consider the scramble U D. We know both U and D have even parity. If we combine them together, that gives us an even + even number of transpositions, and since adding two even numbers gives an even number, U D can be decomposed into an even number of transpositions. In other words, any Rubik’s Cube scramble has even parity.

Why is this useful? Remember that we can describe a scramble of a Rubik’s Cube using $(\sigma, \tau, x, y)$ where $\sigma \in S_8$ and $\tau \in S_12$. An important theorem is that a permutation is valid if $\epsilon(\sigma) = \epsilon(\tau)$. The proof of this is beyond the scope of this reading, but if you have some abstract algebra under your belt, feel free to check it out here. Also notice that half of the elements of a symmetric group have even parity and half of them have odd parity. To consider how many times $\epsilon(\sigma) = \epsilon(\tau)$, we can imagine flipping two coins, and counting the number of times they are both the same outcome. The four outcomes are HH, HT, TH and TT. Half of these have the same outcome for both, so half the time $\epsilon(\sigma) = \epsilon(\tau)$.

To count the number of permutations we start by considering the number of tuples $(\sigma, \tau, x, y)$, which is $12!8!3^82^{12}$ (Why?). We know half the permutations are valid, and another fact is that $1/6^{\text{th}}$ of the orientations are valid. Once again, the proof of this is a beyond the scope of this reading, but is also contained here. So, the number of permutations on of a cube is $\frac{12!8!3^82^{12}}{12} = 43,252,003,274,489,856,000$.

Note that there are easier ways to come to this number, this just uses concepts we discussed.

Commutators #

So far, we’ve used concepts from group theory to understand the structure of the Rubik’s Cube. Now, we move to using group theory to come up with ways to move around pieces in the cube.

Definition of a Commutator #

For two elements, $g, h$ of a group $G$, we define their commutator to be $$[g, h] = ghg^{-1}h^{-1}.$$ This element is equal to the identity $e$ if and only if $g$ and $h$ commute.

For example, consider the Rubik’s Cube Group and the commutator [R U R', D] = R U' R' D R U R' D'. Try doing these moves on a cube! This is what you get:

Notice that this is a cycle of 3 pieces! Why is this useful? Well notice that moving a limited amount of pieces is useful on its own to solve the cube, but we can also construct algorithms using this method. For instance, an E Perm is two commutators.

Conjugation #

Suppose we were working in a factory and there are three stages. Each stage has an item on it which needs to be stamped, but only stage 1 has a stamping machine. However, we are able to swap elements around on the stages. How can we stamp all three items and put them back in their original configuration? We can make use of something called conjugation.

Generally, conjugation of a group element $g$ by an element $h$ is given by $$hgh^{-1}.$$ We can apply this to our factory example as follows. To stamp any of the items, we can simply move it to stage 1, then stamp it on stage 1, then move it back to its original position. This takes the form of conjugation exactly, as $$\text{stamp item X} = (\text{swap 1 and X})(\text{stamp 1})(\text{swap 1 and X})^{-1}.$$ On the Rubik’s cube, we usually refer to this as doing setup moves. For instance, we know how to swap pieces 1 and 2 using an algorithm, but we want to swap pieces 1 and 3 instead. Then we can move piece 3 to the position of piece 2 (this is the setup), execute the algorithm, then undo our setup. This proves to be very useful because of how the setup and algorithm are independent - regardless of how the algorithm works, as long as we swap the pieces beforehand we know what the result will be.