Rubik’s Cube Notation #
Types of Pieces #
The 3x3 Rubik’s cube consists of 27 small cubes known as “cubies.” There are 3 different types of pieces, which can be differentiated based on their position on the cube and their number of faces:
- Center pieces (1 face): These pieces are fixed on the cube, in the center of each face and do not move relative to the other centers. There are 6 center pieces (one for each face).
- Edge pieces (2 faces): These bi-colored pieces form a “cross” on each face of the cube. There are 12 edge pieces, as each layer has 4 pieces.
- Corner pieces (3 faces): These tri-colored pieces make up the 8 corners of the cube.

Center pieces

Edge pieces

Corner pieces
When notating pieces on the cube, we prefer to use the position of each cubie instead of the color of the cubie. We can name each face of the cube using the following directions: up (U), right (R), front (F), left (L), back (B), down (D).
Then we can indicate an edge using two letters and corners using three letters. For instance, the edge in the intersection of the top face and the front face of the cube would be labelled UF. The corner located in the intersection of the top face, the front face, and the right face would be labelled UFR.
In addition, the first letter we give in the notation indicates the orientation of the cubie. In this example, UF indicates the yellow face of the yellow/blue edge while FU indicates the blue face in the cube state below. This is similar for corners.

The yellow facelet/sticker of the blue/yellow edge is called
UF.

The yellow facelet/sticker of the blue/red/yellow edge is called
UFR.
Types of Moves #
Now that we can refer to individual pieces, we now will learn to refer to individual moves. Each move involves is a type of rotation. By default, this rotation is a clockwise quarter-turn. So for instance, R signifies turning the right face clockwise by 90 degrees. Furthermore, “clockwise” describes the direction of the face when looking directly at it. So the direction of R and L are opposite since clockwise means a different direction when looking at the right and left faces.
Furthermore, moves can be modified using a ' (prime) and number. The ' signifies inverting the move, or turning counter-clockwise instead of clockwise. Meanwhile, adding a number after the move means doing the move that number of times (ex. R2 means doing R then R again). It may be helpful to note that R2 = R2' and U3 = U'.
Moves break down into a few types:
- Single face turns (
U,R,F,L,B,D): These moves turn a single face of the cube. These will be the moves you probably use most frequently. - Wide turns (
u,r,f,l,b,d): These moves involve turning two layers of the cube at the same time. For instance,uturns both the top face and the middle layer at the same time by a quarter-turn. - Cube rotations (
x,y,z): These moves involve rotating the entire cube such that the cube state remains the same, but the orientation of the cube changes. - Slice moves (
M,E,S): These moves only move the middle “slice” of the cube. There are three slice moves to correspond to the three slices of the cube. Oddly enough, the direction ofMmoves actually follow the direction ofLmoves,EwithD, andSwithF
The dropdown below houses a simplified photo version of notation mapped to moves.
Notation (photo)
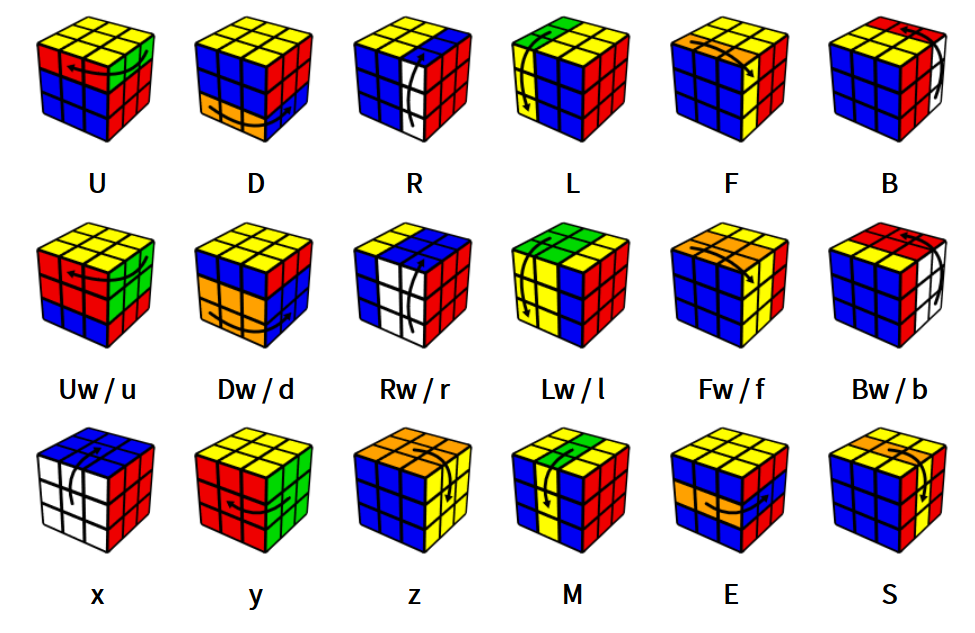
The dropdown below houses an animated version of notation mapped to moves.
Notation (animation)
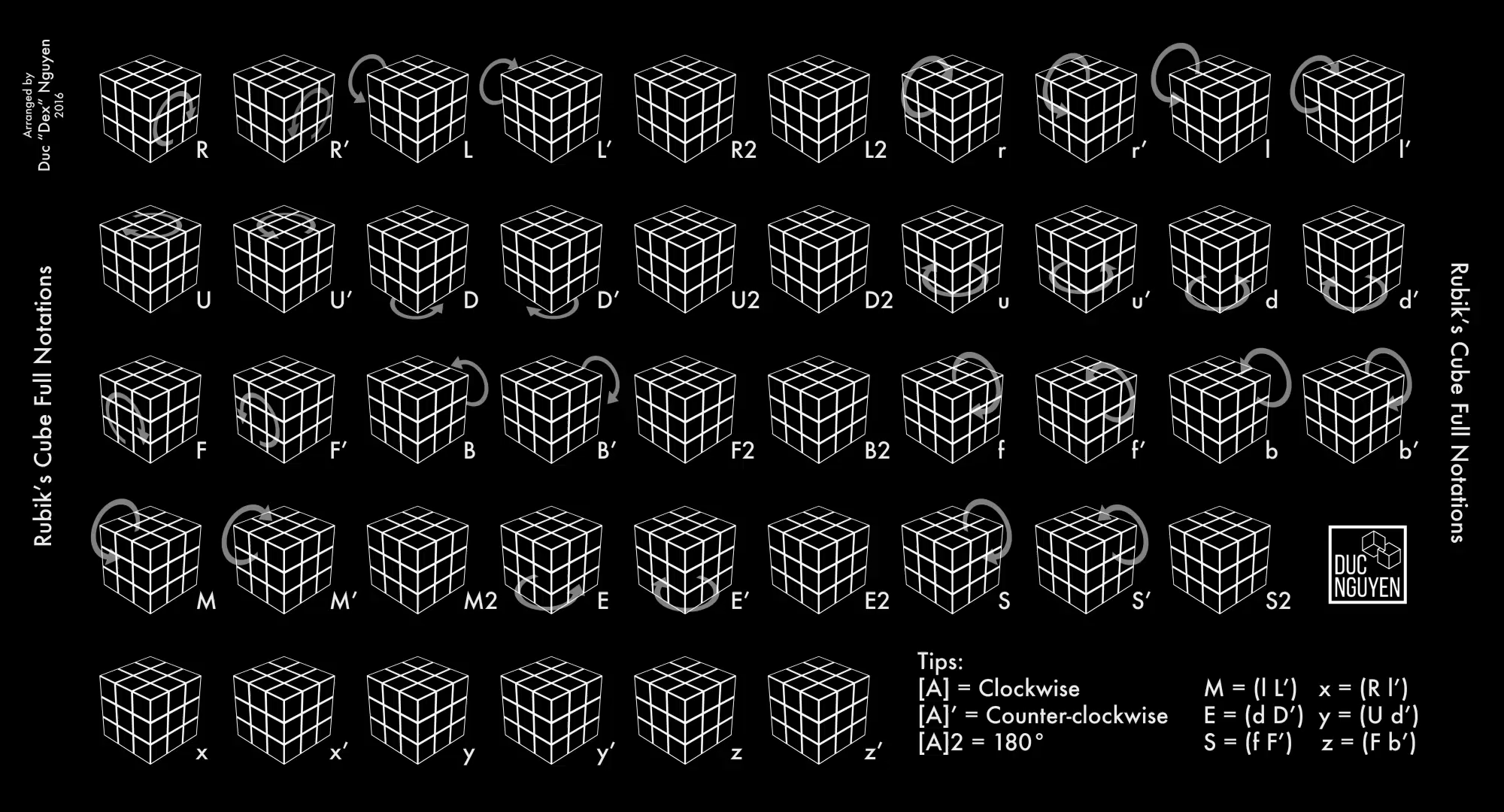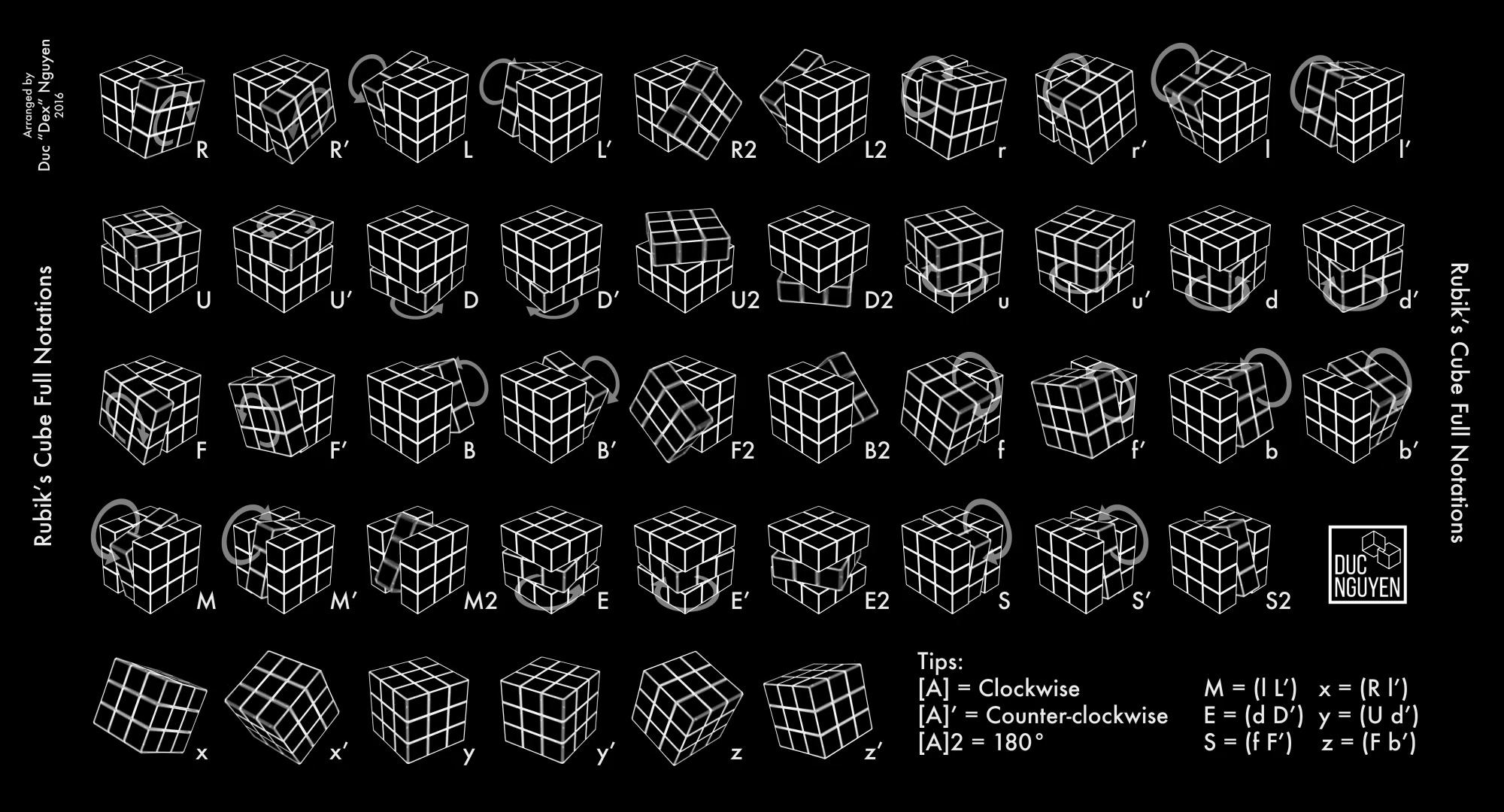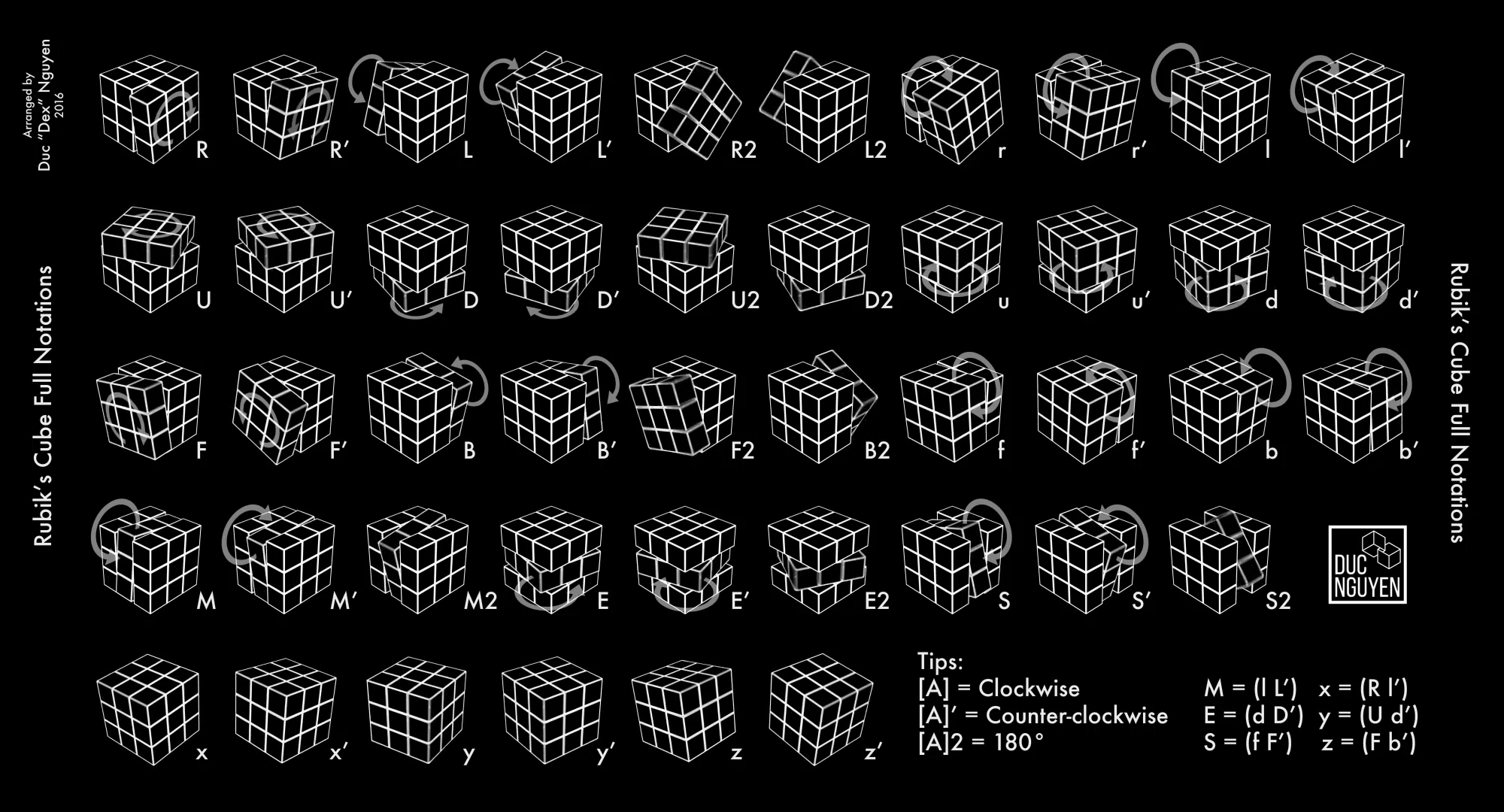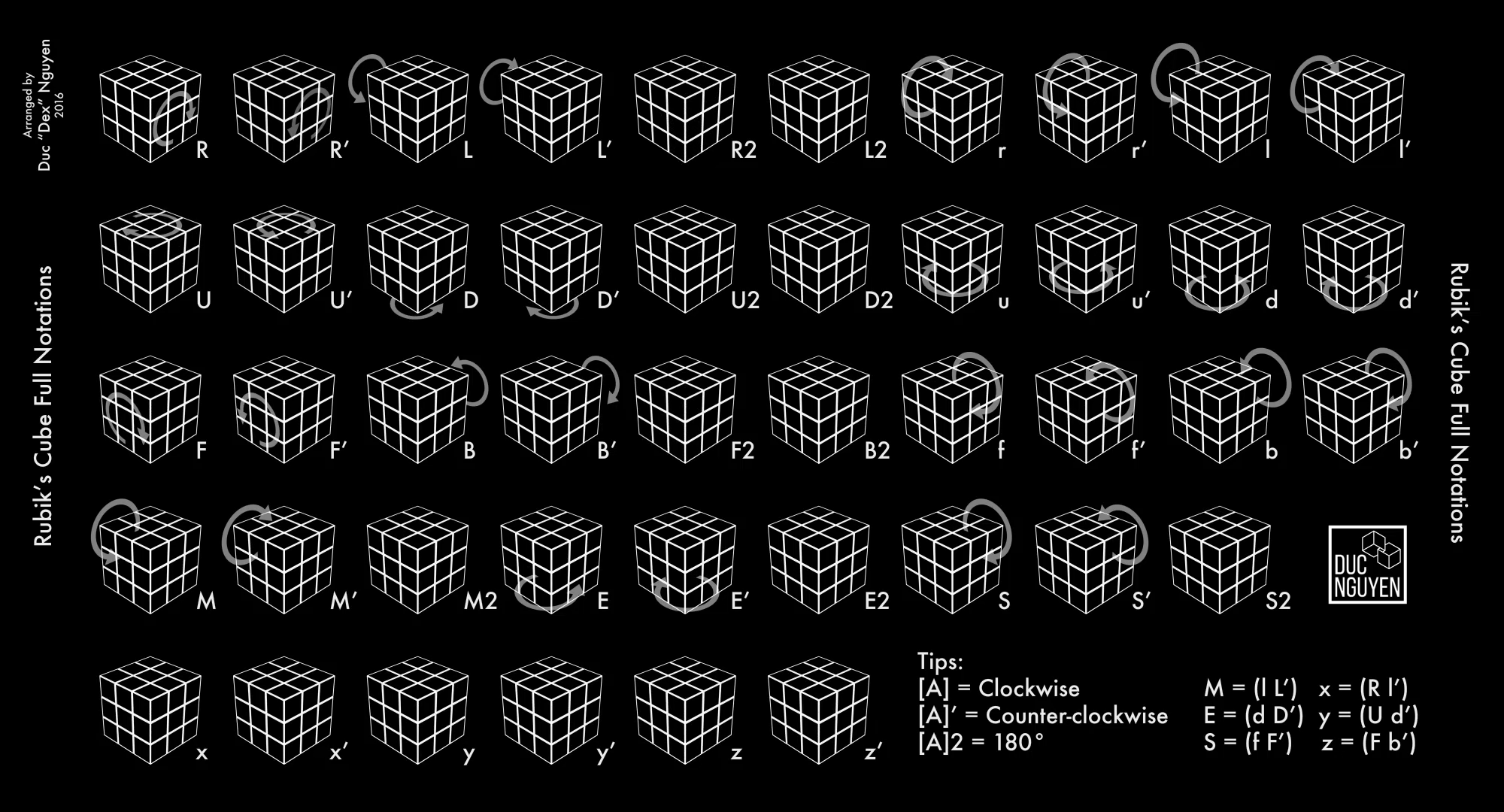
Groups #
Groups are a simple, abstract mathematical structure which can describe a broad range of applications. The advantage of using the abstract group is to show results for a single abstract group that hold for all groups. That is, by proving a property of groups, we are able to say something about all applications that fit the structure of the group, including the Rubik’s Cube.
Definition of a Group #
A group \((G, *)\) consists of a set \(G\) (an unordered list of elements) and a binary operation \(*\) (a function which takes two elements of \(G\) and maps it to another element of \(G\) ) which satisfy the following properties:
- Closure: If $a$ and $b$ are elements of $G$, then $a * b$ is also an element of $G.$
- Associative: $*$ is an associative operation, meaning $(a * b) * c = a * (b * c)$ for all $a, b, c$ in $G$.
- Identity: There exists an identity element $e$ in $G$, such that $a * e = e * a = a$ for all $a$ in $G$.
- Inverse: For all $a$ in $G$ there exists an inverse element $a^{-1}$ such that $a * a^{-1} = a^{-1} * a = e$.
Furthermore, a group is abelian or commutative if it satisfied commutativity, meaning $a * b = b * a$ for all $a, b$ in $G$. In addition we will sometimes omit the group operation and write $ab \equiv a * b.$
Examples of Groups #
Consider the following examples of groups:
- $\mathbb{R}$ (the set of all real numbers) is a group under addition $+$. How do we know? First, addition is associative by definition. The identity element is $e = 0,$ since $x + 0 = x$ for any real number $x$. The inverse element $a^{-1} = -a$ since $a + (-a) = 0$ for any real number $a$ in $\mathbb{R}.$
- $\mathbb{Q}^+$ (the set of all positive rational numbers) is a group under multiplication $\times$ with $e = 1, a^{-1} = \frac{1}{a}.$
The Rubik’s Cube as a Group #
We can describe the set of moves on the Rubik’s Cube as a group
$(\mathbb{G}, *)$ with the binary operation composition. An element of
$\mathbb{G}$ will be the set of all possible moves of the Rubik’s Cube
(one example would be $M =$ R2 U). The group operation
will be defined as follows: if $M_1$ and $M_2$ are both moves, then
$M_1 * M_2$ is the move where you first do $M_1$, then do $M_2$. Two
moves are considered the same if they result in the same configuration
of the cube. We can show this is a group by going through the
definition:
- Closure: If $M_1$ and $M_2$ are moves on the Rubik’s Cube, then $M_1 * M_2$ (which is doing one move, then the other) is also a move on the cube.
- Associativity: This is slightly tiresome to show rigorously, so we will make a basic argument for associativity. Regardless of how we group the moves together, as long as we make the moves in the same order the outcome is unchanged.
- Identity: $e$ will be the "empty" move, which is doing nothing to the cube.
- Inverse: For a move $M$, we can reverse the steps of the move to get
$M'$, and find $M * M' = M' * M = e.$ For instance, the inverse of
R U L' DisD' L U' R', which we find by inverting the moves from the end.
Theorems About Groups #
Here are some simple theorems about groups which can be derived from the axioms for a group $(G, *)$:
-
If $a * b = e$, then $a = b^{-1}.$
-
The identity element $e$ is unique.
-
If $a * x = b * x,$ then $a = b$.
-
The inverse of $(a b)$ is $b^{-1}a^{-1}.$
A Quick Proof #
We will briefly prove the first theorem. A proof about groups should
start using only what we already know about groups (in this case,
the definition of a group) to show our desired result.
Our initial assumption is that $a, b$ are elements of a group $G$ and we
want to show $a * b = e$ implies $a = b^{-1}.$ Since we know $G$ is a
group, from the inverse property we know there exists $b^{-1}$ in $G$
such that $b * b^{-1} = e.$ Then we can multiply on the right of both
sides of the equality by $b^{-1}$ to find the following:
| # | Step | Reasoning |
|---|---|---|
| 1 | $a * b = e$ | by assumption |
| 2 | $a * b * b^{-1} = e * b^{-1} $ | right multiply by the inverse of b |
| 3 | $a * (b * b^{-1}) = b^{-1}$ | by the definition of the identity |
| 4 | $a * e = b^{-1}$ | by the definition of inverses |
| 5 | $a = b^{-1}$ | by the definition of the identity |