Permutations #

Suppose you had three tasks to do by the end of the night: eat, do homework, and study. You could do these tasks in any order, but only one at a time. That is, you could eat, do homework, then study (eat, HW, study), or first study before doing homework, then eating (study, HW, eat), and so on. Each of these orderings would be a single permutation of the events.

More generally, a permutation is an arrangement of elements into a sequence. If we started with $N$ boxes, labeled $1$ through $N$ and one objects in each box labeled in the same way, we can think of a permutation as taking out the objects and putting them back into the boxes in some arrangement. So we can describe a permutation as:

1. The object originally in box 1 was moved to box $A_1$.

2. The object originally in box 2 was moved to box $A_2$.

3. The object originally in box 3 was moved to box $A_3$.

and so on, where $A_1, A_2, …$ are all numbers from $1$ to $N.$

Two Line Permutation Notation #

We can represent the permutation in a more compact form using two-line notation: \[\begin{pmatrix} 1 & 2 & 3 & 4 &...& ...& N \\ A_1 & A_2 & A_3 & A_4 &... & ...& A_N \end{pmatrix},\]

where the top row is the number of each box and the bottom row is the element which ends up in that box.

Canonical Cycle Notation #

Two line notation can be a bit repetitive, since the top row is always just $1, …, N.$ Hence, we can write this in a more efficient manner, known as canonical cycle notation. For the cycle $$\begin{pmatrix} a_1 & a_2 & a_3 & a_4 &… & …& a_{m_1} \end{pmatrix},$$ we would interpret this as:

1. The object originally in box $a_1$ was moved to box $a_2$.
2. The object originally in box $a_2$ was moved to box $a_3$.
3. The object originally in box $a_3$ was moved to box $a_4$.

and so on, except for the last element in box $a_{m_1}$ is moved to box $a_1$. Notably, this can only describe a single cycle, as the last element $a_{m_1}$ must be moved to the position of the first element $a_1$. Visually, this can be shown as follows:

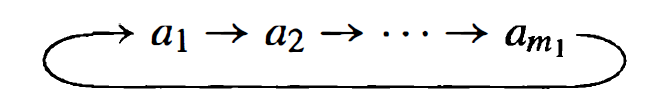
We can string together different cycles to generate arbitrary permutations. For instance, we can write $k$ different cycles of lengths $m_1, m_2, …, m_k$ by stringing them together: \[\begin{pmatrix} a_1 & a_2 &...& a_{m_1} \end{pmatrix} \begin{pmatrix} a_{m_1 + 1} & a_{m_1 + 2} & ...& a_{m_2} \end{pmatrix}... \begin{pmatrix} a_{m_{k-1} + 1} & a_{m_{k-1} + 2} & ...& a_{m_k} \end{pmatrix}. \] This can be visualized in a similar fashion:

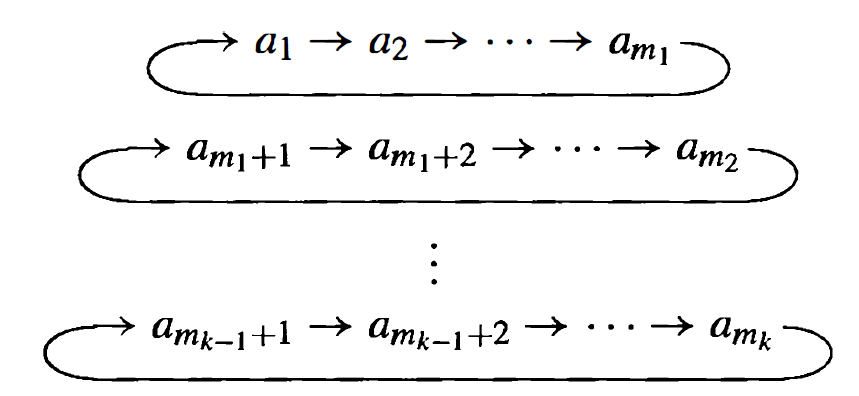
If two cycles share no elements, they are called disjoint cycles. Any permutation can be written as an arbitrary combination of disjoint cycles.

Example Cycle Decomposition #

Let’s say we define a permutation with 5 elements ${ 1, 2, 3, 4, 5 }$ with the following rules:

1. 1 goes to 2
2. 2 goes to 3
3. 3 goes to 1
4. 4 goes to 5
5. 5 goes to 4

To write this in canonical cycle notation, we start with 1, which goes to 2, giving us $(1 \ 2$, then add 3, and noticing it goes back to 1 so we can complete the cycle, giving us $(1\ 2\ 3)$. Similarly, 4 goes to 5, giving us $(4\ 5$, and noticing that 5 goes back to 4, we can complete the cycle, leaving us with $(1\ 2\ 3) (4\ 5)$

Symmetric Group #

Actually, the set of all possible permutations on $n$ elements forms a group known as the symmetric group, $S_n$. We define the binary operator to be function composition, $\circ$. So for two permutations $\sigma, \tau\in S_n$, we have $\sigma \circ \tau$ meaning we first reorder the elements using the permutation $\tau$, then we reorder the resulting elements using $\sigma$.

Order and the Symmetric Group #

Recall the order of a group $G$ is given by $|G|$ and it represents the number of unique elements in the group. In our case, $|S_n|$ is the number of unique permutations on a set of $n$ elements. This number can easily be found using combinatorics to be $n!$, which is defined as $$n! = n\cdot(n-1)\cdot(n-2)\cdot …\cdot 3\cdot 2\cdot 1.$$ The order of elements in $S_n$ is trickier. First, let’s consider the order of a single cycle of length $\ell$, given in canonical cycle notation by $\sigma = \begin{pmatrix} a_1 & a_2 & a_3 & a_4 &… & …& a_{\ell} \end{pmatrix}.$ For $\sigma^n = e$, we require all elements to be in their original position. We know after applying $\sigma$ one time, we have element $a_1$ moving to the position of $a_2$. Then after the second time, $a_1$ is in the position of $a_3$. We can continue this process to find that $\sigma^\ell = e$, implying $|\left<\sigma\right>| = \ell.$ That is, the length of a cycle is the same as its order.

Since any arbitrary permutation $\tau$ can be written as a product of cycles $\sigma_1 \sigma_2… \sigma_k$ for some $k$, we can find the lengths of those cycles $\ell_1, \ell_2, …, \ell_k$. Then the order of $\tau$ is the least-common multiple of these elements: $$|\left<\tau\right>| = \text{lcm}(\ell_1, \ell_2, …, \ell_k).$$

Inverting Elements of the Symmetric Group #

Given a permutation $\sigma$, how can we find $\sigma^{-1}?$ Intuitively, this is simple. If we took all the objects and moved them around, then just do the opposite of what you just did, and put them back where the used to be. Furthermore, we can do this in parts once again. If we can invert a single cycle, we can simply invert each cycle in the permutation to invert the permutation.

Once again, consider a single cycle of length $\ell$, given in canonical cycle notation by $\sigma = \begin{pmatrix} a_1 & a_2 & a_3 & a_4 &… & …& a_{\ell} \end{pmatrix}.$ Here, Figure 1 can aid our intuition of how to invert this cycle. We know that to do the opposite of this action, we simply flip all the arrows in Figure 1. Then, we can rewrite this in canonical cycle notation as $$\begin{pmatrix} a_\ell & a_{\ell-1} &… & …& a_2 & a_1 \end{pmatrix}.$$ So, inverting a cycle is the same as reversing the order of the elements when written in canonical cycle notation.

For example, consider $\sigma \in S_5$, where $\sigma = (3\ 1\ 4\ 2\ 5)$. Then, $\sigma^{-1} = (5\ 2\ 4\ 1\ 3)$.

Composition of Permutations Example #

To compose permutations, we apply them from left to right. Consider permuting $\sigma, \tau \in S_5$. Let $\sigma = (1\ 2\ 3)(4\ 5)$ and $\tau = (3\ 1\ 4\ 2\ 5)$. To solve $\sigma \circ \tau$, we consider passing each element through $\tau$ then $\sigma$. If you’re familiar with function composition, for each element $i$, $(\sigma \circ \tau)(i) = \sigma(\tau(i))$.

1. $1 \rightarrow 4 \rightarrow 5$
2. $2 \rightarrow 5 \rightarrow 4$
3. $3 \rightarrow 1 \rightarrow 2$
4. $4 \rightarrow 2 \rightarrow 3$
5. $5 \rightarrow 3 \rightarrow 1$

So, the final result is $\sigma \circ \tau = (1\ 5)(2\ 4\ 3)$.

The Rubik’s Cube And Permutations #

Using elements of symmetric groups, we can actually come up with a representation for the state, or a scramble, of the Rubik’s Cube. Typically, we represent scrambles using R, U, R', F', etc. but there are certain limitations to this notation. It’s great for scrambling and learning algorithms but how would one count permutations of a Rubik’s Cube with this notation? It’s a non-trivial task; a permutation is not just a sequence of R moves followed by U moves followed by F moves and so on (called a linear combination, which is fairly easy to count), but rather some combination of moves in any order.

But, before we talk about this new representation, let’s recall notation for describing pieces on a cube.

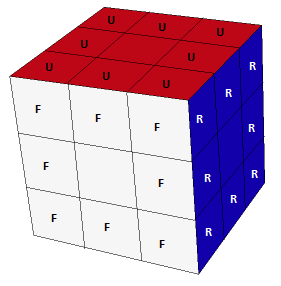
Take a look at this picture, which assigns each face of the cube a letter. Using this, we can describe edge pieces using the two face that they touch, and describe corner pieces with the three faces that they touch. For example, in this picture the red-white edge can be UF and the red-white-blue corner can be UFR.

In order to describe one permutation of the cube, we need to describe 4 different things:

1. The positions of each of the corners (which of the 8 positions is each corner in?)
2. The orientations of each corners (what orientation is the corner twisted to?)
3. The positions of each of the edges (which of the 12 positions is each edge in?)
4. The orientations of each of the edges (are any of the edges flipped?)

Consider the first one. Imagine 8 different slots and we choose one corner for each slot. Well, this is just a permutation! We can describe the position of corners as $\sigma$, an element of $S_8$. Similarly, we are trying to place 12 different edge pieces into 12 different slots, meaning the edge positions can be described using $\tau$, an element of $S_{12}$.

You might notice that we haven’t taken into account permutations that are invalid. For instance, swapping just two edges isn’t a valid configuration, but that permutation is still described by an element of $S_8$. However, reducing the problem to evaluating elements of $S_8$ is a valuable step, as we’ve transitioned form thinking about combinatorics to a more algebraic approach.

Describing the orientations of each piece is left as a challenge for you. Think about how you can use a number from ${0, 1, 2}$ to describe corner orientations and a number from ${0, 1}$ to describe edge orientations.